15  Introduction to basic solid mechanics

Solid mechanics or mechanics of materials is the study of the relations between forces acting on a solid body and causing strains and stresses. In this chapter we will introduce mechanical properties in order to be able to dimension parts to withstand given loads without failure.

Compared to forces, stress is a better measure to gauge the strength of a material from which the body is made of. Using force (or the completely misplaced term weight in some forums) as a measure of how much force a solid body can carry before it fails is troublesome since that depends on the size of the object, more precisely it depends on the load carrying area. By dividing the force by the area we get stress which is a better measure for comparing mechanical properties of a material. More on this topic can be found in the next section.

A thorough understanding of the fundamentals of solid mechanics is crucial for the design of any machine or structure.

Conducting analysis by hand as the primary tool for structural analysis is a thing of the past, modern engineers need to focus on the study of the problem statements and primarily creating and verifying the models. The human factor, the engineer, sets up the problem by posing the governing equations, load cases thorough boundary conditions and loads, sets up assumptions and simplifications, in short, creates a computational model of the physical model. Then we must let the computer do the actual computations, the solution of the resulting system of equations and any parameter studies and visualizations. This is what machines excel at. The computations are less error prone, more accurate and much much faster. The engineer needs to focus on the computational thinking [see 1] to produce results. In this course we shall focus on the modeling and we will be freeing up time to explore more fun problems, real-life problems that traditional courses lack since it is hard or impossible to solve them by hand and instead we simplify problems and create these academic problems which are never found in real life engineering applications.

As we shall see, too many problems are hard to simplify and solve using special cases that can be calculated by hand. Instead we need to familiar ourselves with the general cases expressed in term of partial differential equations and solved using numerical methods in commercially available software packages such as SolidWorks Simulation, LS-Dyna or Ansys. The software packages are based on the Finite Element Methods (FEM) and the process of creating load cases and analys is known as Finite Element Analysis (FEA).

Solid mechanics always starts with a mechanical analysis and a free body diagram. Let us use a simple example using a body which has two or three supports and is subjected to a force. A body using two supports can be solved using mechanics alone, the reaction forces can easily be determinate from force-, and moment-equilibrium.

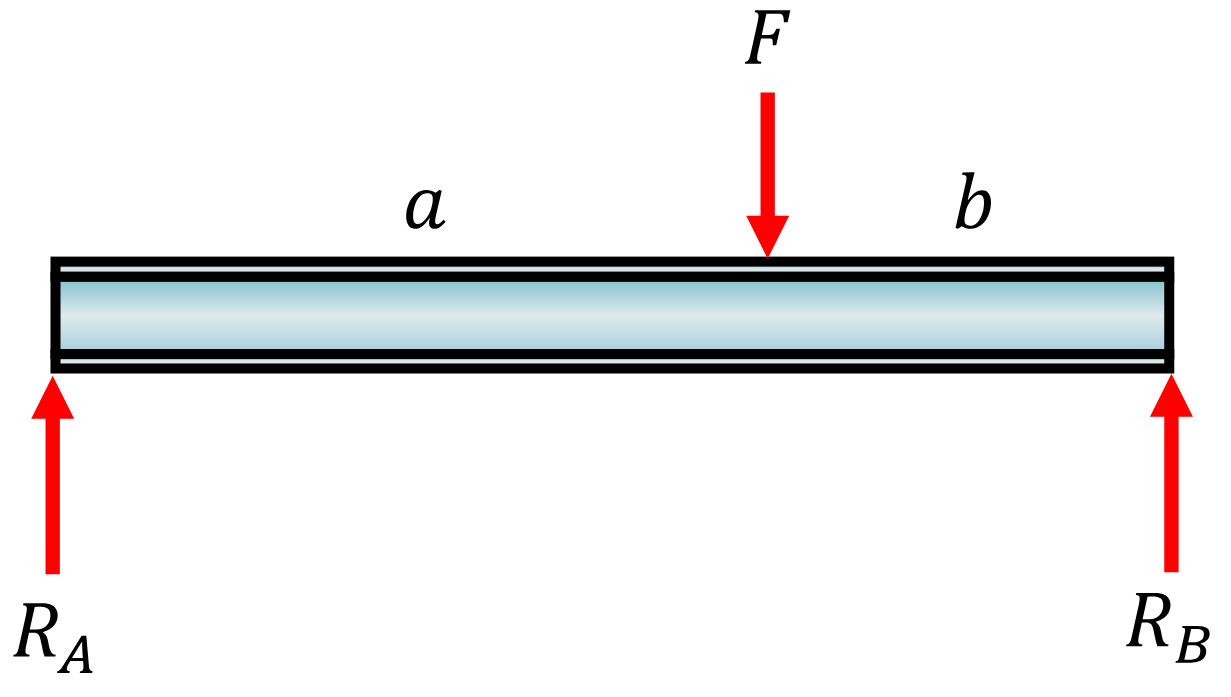
We get two equations and two unknowns, \(R_A\) and \(R_B\). The system is statically determinate.

import sympy as sp

R_A, R_B, F, a, b = sp.symbols('R_A, R_B, F, a, b', real=True)

eqs = [sp.Eq(R_A + R_B -F,0),
       sp.Eq(a*-F + (a+b)*R_B,0)]

$$ \begin{align*} - F + R_{A} + R_{B} = 0 \\ - F a + R_{B} \left(a + b\right) = 0 \end{align*} $$

15.1 References

[1]

Wing JM. Computational thinking. Commun ACM 2006;49:33–5.